HÌNH HỌC KHÔNG GIAN

2024-09-21 15:19:32  112  0  Báo cáo

 0

 0

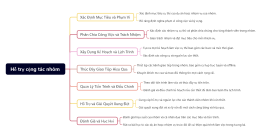
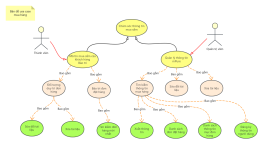
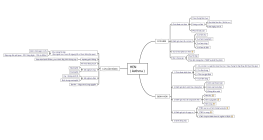
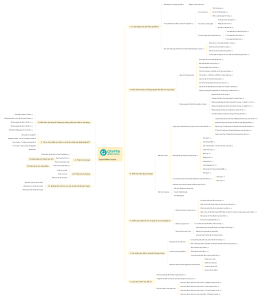
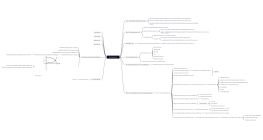
Sơ đồ tư duy này cung cấp một cái nhìn tổng quan chi tiết về hình học không gian, bao gồm các khái niệm cơ bản và phương pháp chứng minh. Nội dung bao gồm định nghĩa và ký hiệu của hai mặt phẳng vuông góc, cách chứng minh hai mặt phẳng vuông góc, góc giữa đường và mặt phẳng, cách xác định góc tạo bởi đường và mặt phẳng, khoảng cách từ một điểm tới mặt phẳng, và định nghĩa cùng cách chứng minh đường vuông góc với mặt phẳng. Các bước chi tiết và ký hiệu rõ ràng giúp người học dễ dàng nắm bắt và áp dụng kiến thức vào bài tập và thực tế. Sơ đồ tư duy này là công cụ hữu ích cho học sinh và giáo viên trong việc giảng dạy và học tập hình học không gian, đảm bảo hiểu rõ các khái niệm và phương pháp chứng minh một cách hiệu quả.

Tác phẩm khác của tác giả

Dàn ý / Nội dung

3. Hai mặt phẳng vuông góc

Định Nghĩa

Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°

Kí Hiệu

(α) ⊥(P)

Cách c/m (α) ⊥(P)

Chọn d ⊂ (α)

d ⊥ (P)

2. Góc của đường và mặt phẳng

Định Nghĩa

Nếu đường thẳng d không vuông góc với mặt phẳng (α) thì góc giữa đường thẳng d và mặt phẳng (α) bằng góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng .

Nếu đường thẳng vuông góc với mặt phẳng thì ta góc giữa đường thẳng và mặt phẳng bằng 90°.

Kí Hiệu

(d,(α))

Cách Xác Định Góc Tạo Bởi d và (α)

B1: Xác Định Điểm Chung của d và (α)

B2: Xem đường thẳng S nào vuông với mp (α)

B3: Ghi góc ra theo trình tự "điểm chung" nằm giữa đường thẳng "s nào vuông với mp (α)"

4. Khoảng cách từ một điểm tới mặt phẳng

1. Đường vuông góc với mặt phẳng

Định Nghĩa

Đường thẳng d được gọi là vuông góc với mặt phẳng (α) nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (α)

Kí Hiệu